Set-Ups:
Case 1: For this case, my group and I set up the constant to be the Temperature. Then, we set different volumes for the container in which the particles were held, and then from there, we recorded the volumes of the container as well as the corresponding pressures, which led to the realization that Volumes and Pressures have an inverse relationship.
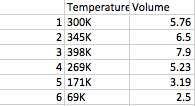
Case 2: The constant was the Pressure. So, with that pressure, my group and I raised and lowered the temperature in Kelvins, and then we noted how the Temperature and Volume had a direct relationship.
Case 3: The constant, in this case, was the volume. So, for a given volume, we moved the temperature up and down and saw how the pressure reacted when the temperature was being moved, and found that it was a direct relationship as well.
Case 4: In this instance, we had two constant variables: the temperature and the pressure. With this one, we adjusted the amount of particles that were in the space, but since the volume wasn't fixed, it moved itself to adjust for the particles in the space. This relationship, like the last two, is direct.
Questions:
3. See below
4a. Bicycle tires seem flatter because the temperature decreases from the summer to the winter, and as the temperature decreases, the volume will decrease. This is a case of Charles's Law.
4b. In the summer, if a soda can is left out, the temperature around the can increases, which in turn makes the pressure increase, according to Gay-Lussac's Law.
4c. As the temperature of the gas decreases, as a temperature of an object does when the object is placed in ice, it'll decrease the pressure (according to Gay-Lussac's law), but the volume will stay the same as the container is "rigid," and being placed on ice will not change the natural size of the container.
4d. This treatment will not help because as the temperature increases by means of treating the area with moist heat, the pressure will also increase, and since pressure last time caused a toothache, there's no reason to think that increasing pressure (by means of moist heat) this time will alleviate the pressure unlike last time.
Data:
(Case 1 data)
(Case 2 data)
(Case 3 data)
 |
Case 4 data
|